Introduction
A few decades ago, the title of this article might have seemed like an oxymoron. However, perceptions have since evolved [1]. This series of articles argues that C++ templates are uniquely positioned to allow developers to “have their cake and eat it too”. In other words, they enable the creation of high-level coding abstractions similar to those in MATLAB or Python, which not only promote significant reuse and rapid implementation for complex signal processing architectures, including nonlinear processing and machine learning, but also offer flexibility, modifiability, and manageability. At the same time, they achieve code size and computational efficiency comparable to hand-crafted code, making them suitable even for the most resource-constrained environments, such as low-power microcontrollers with only a few kilobytes of memory. For the latest version of the signal processing library and full details of the code examples discussed here, see [2].
The platform independent templates support a coding style suited for high-reliability, high-performance, resource-constrained embedded applications that may choose to avoid dynamic memory allocation or only use a heap during startup initialization. For maximum performance, these applications also often choose to disable exception handling. Additionally, they may avoid standard libraries that significantly increase RAM or ROM requirements, dynamically use the heap, require exception handling, or significantly increase application code and data memory space requirements. Computing platforms can range from no operating system super-loops on a miniature microcontroller to standard operating systems such as Windows or Linux. This style also typically provides unmatched performance and resource efficiency for standard platform applications.
Additionally, we prioritize logical, object-oriented design and interface simplicity with direct template methods over more complex template meta-programming approaches, unless the latter offers a significant advantage. In such cases, we aim to provide thorough comments to ensure that even those who are not experts in templates can follow the logic, particularly during debug.
Good linear algebra capabilities are important, with MATLAB or NumPy-like abstractions supporting vector/matrix arithmetic (e.g., C = A + B, where A, B, and C are arrays, vectors, matrices, or tensors). For our implementations, we chose the C++ library Eigen [5] to provide excellent linear algebra capabilities. Although Eigen can run on platforms like Arduino, it might be criticized for inefficiency in debug mode or its complex internal template metaprogramming, especially when one tries to resolve compiler errors or find code bugs. To address these shortcomings, we provide simpler alternative matrix/vector options that can be mixed and matched with Eigen or even used to avoid Eigen. These classes offer a simpler view of the same underlying raw data used by an Eigen matrix, allowing data to be passed to and from Eigen without data copies.
While Eigen is efficient for processing data from files or stored in large buffers, without additional techniques it is not efficient for realtime, namely online signal processing of continuous data flow. Efficient online processing requires operators that maintain and update internal state iteratively as new data arrives, as well as ring buffers between algorithm operators to minimize data copies and to keep computation latencies from varying with time. Buffers should not increase with processing increasing amounts of data, as might occur if internal buffers grow via dynamic allocation, for example.
Figure 1 conceptually illustrates a complex and challenging general computational pipeline, whose efficient implementation is the objective
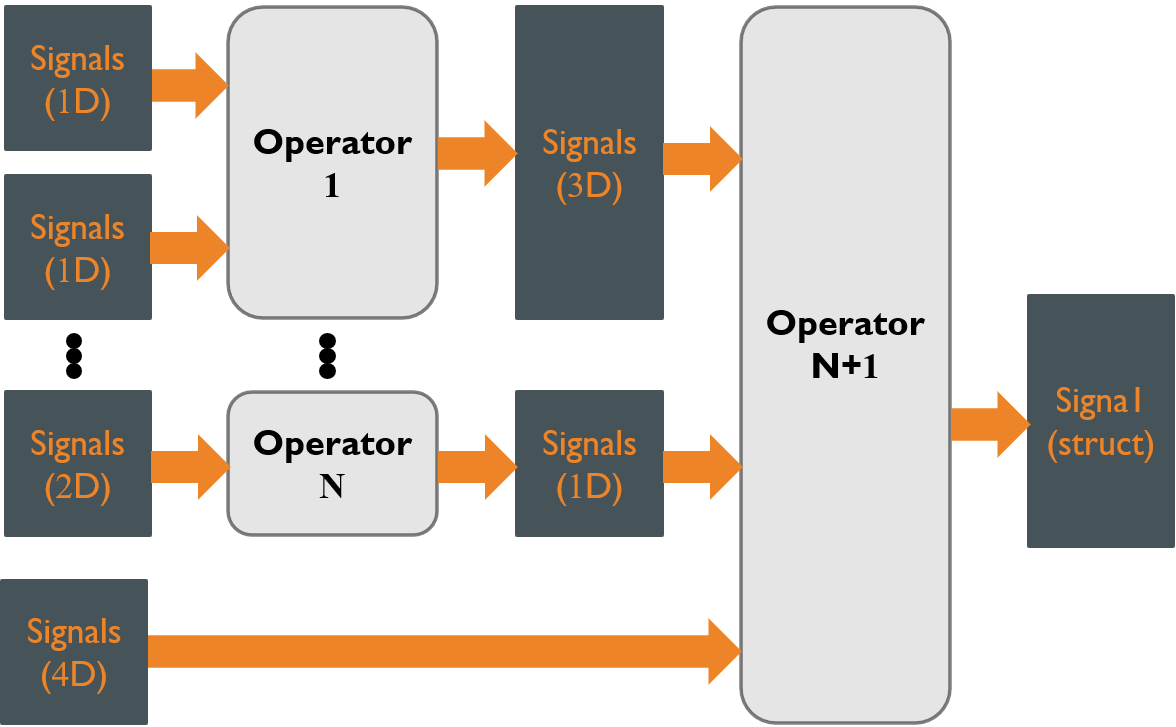
Figure 1: Conceptual signal processing pipeline
for our template building blocks. The pipeline handles continuous streaming of 1D, 2D, 3D, or nD array signals, such as sound or images, as well as signals where each time sample is an application-specific data structure, like the features of human beings detected in a video stream. Namely, a signal is any datatype generated iteratively or repetitively over time, such as a vector, matrix, tensor, or data structure, where one of the signal dimensions represents time. Each signal can consist of varying numbers of data channels processed by different operator types, either in parallel or in series. The data may have different sample rates or be spaced at non-uniform time intervals.
Signal processing operators can increase (interpolate) or decrease (decimate) data rates or convert a uniform input rate to a non-uniform output rate. An example is an output feature stream of a physiological signal such as ECG whose features synchronize with the nonuniform period of the human heart. The pipeline can be hierarchical, meaning another complex pipeline might be the internal implementation for a signal processing operator. To minimize latency and maximize throughput, it should be possible to allocate operators to different threads easily as well as change thread allocation. Support must be provided for time, time coordination, time errors, or data errors.
A good approach to understand a complex pipeline implementation strategy using templates is to begin with relatively simple tasks, such as implementing a network of multi-channel, linear digital filters. We will then demonstrate in later installments how the same or related template techniques can be extended to increasingly complex operators or pipeline types that could include nonlinear Kalman filters, optimization operators, machine learning classifiers, etc. Starting with simple examples, such as realizing a digital filter with a multi-channel array input and multi-channel array output, also ensures that the design strategy does not require the setup of overly complicated or extensive general machinery to do something that is relatively simple and straight-forward.
Sharpened Filter Pipeline
As a starting example we will show how to implement an effective digital filter with very few multiplications using “Filter sharpening” [3][4]. A sharpened filter is inherently a signal processing pipeline, and this signal processing technique is also particularly well suited for fixed-point arithmetic implementations, where it can implement filters having good time and frequency characteristics with almost no multiplications required.
Sharpening starts with a linear filter represented by its Z-transform transfer function, H(z), (we will drop the z for clarity) and forms a new filter by arranging the same H in serial or parallel stages and possibly weighting the output data of one stage before it goes into the next. A polynomial transfer function, P(H), is associated with the overall filter structure. A simple example is the same digital filter concatenated in series, where the resulting filter then has the second order polynomial transfer function, P(H) = H2. The following polynomial structure represents a particularly effective filter,
P(H) = 6H10 – 15H8 + 10H6 Eq. 1
This polynomial represents filter magnitude |H| were we dropped the magnitude bars for clarity. See figure 2 for the complete structure and [3][4] for more detail on the method.
Now suppose H is a computationally efficient filter such as a running sum of N samples, sometimes called a “boxcar”. An efficient implementation would add the latest input sample to the running sum and subtract the oldest sample saved as state, using just one add and one subtract, but no multiplies to compute each output sample. See method TArray operator()(const TArray& in) in the following FilterBoxcar listing.
template<class TArray>
class FilterBoxcar : public DSP::FilterBase<TArray> {
public:
// The basic array type and number type traits currently being used.
using value_type = TArray; // A Boost lib convention.
using Scalar = typename Math::TraitsNumber<TArray>::value_type; // Eigen convention.
struct Config
{
int N; // Length of running sum.
Scalar val; // Initial val for each state.
Config(const Config& c) : N(c.N), val(c.val) { }
Config(int N = 0, Scalar val = 0) : N(N), val(val) { }
};
FilterBoxcar() = default;
virtual ~FilterBoxcar() = default;
bool Set(const Config& c) { cfg = c; return true; }
bool Get(Config& c) const { c = cfg; return true; }
// pS is the pointer to the state array that must be provided by the
// caller and have stateLen contiguous array elements.
bool Init(const Config& c, TArray *pS, int stateLen)
{
bool status = true;
cfg = c;
pState = pS;
maxN = stateLen;
if (cfg.N > stateLen) {
DebugPrintf("FilterBoxcar: Warning, cfg.N=%d > maxN=%d not allowed.",
cfg.N, stateLen);
cfg.N = stateLen;
DebugPrintf("FilterBoxcar: cfg.N=%d set equal to maxN=%d.", cfg.N, maxN);
status = false;
}
// Initialize state.
SetConstant(sum, 0);
for (size_t i = 0; i < cfg.N; ++i) {
SetConstant(pState[i],cfg.val);
sum += pState[i];
}
idx = 0;
return status;
}
#pragma warning(default : 4263)
/// Compute one sample of output from one sample of input.
TArray operator()(const TArray& in)
{
sum -= pState[idx]; // Subtract the oldest.
sum += in; // Add the newest.
pState[idx] = in; // Save the newest.
Inc(idx);
return sum;
}
/// Compute one sample of output from one sample of input. This form of the
/// operator needed for usage of this filter in a template.
int operator()(TArray& out, const TArray& in)
{
out = operator()(in);
return 1;
}
/// Return the running average value of the last N samples. Provide 'out'
/// as the memory for the calculation, which is then also the output.
TArray Average(TArray& out) const
{
out = sum;
out /= static_cast<Scalar>(cfg.N);
return out;
}
// Return DC gain.
virtual Scalar GainDc() const { return static_cast<Scalar>(cfg.N); }
// Return time delay in number of sample periods.
virtual Scalar Delay() const { return static_cast<Scalar>(cfg.N - 1) / 2.0; }
protected:
TArray sum{};
private:
Config cfg;
TArray* pState = nullptr;
size_t maxN=0;
size_t idx=0;
// Circular state buffer index increment.
void Inc(size_t& i) const { i = ((i + 1) == cfg.N) ? 0 : i + 1; }
};Template parameter class TArray is any multidimensional data entity – vector, matrix, tensor, array, etc. In addition, it could also be any primitive built-in type such as double or float.
Note that FilterBoxcar requires its state memory to be provided externally using Init(const Config& c, TArray *pS, int stateLen). For our library, an Init() method is a standard interface design pattern, i.e. a convention for many objects. Static object initialization order is not under the programmer’s control in C++ due to static constructors being called during application launch before the call to main(). Our standard style Init() methods allow the programmer to regain control of initialization order for statically instantiated objects. The fields of the Config struct are specific to the particular filter.
Using the template parameter TMaxStates, the following template class FilterWithState provides state memory without using any heap allocation for its filter class parameter TFiltBase.
template<class TFiltBase, int TMaxStates>
class FilterWithState : public TFiltBase {
public:
using TArray = typename TFiltBase::value_type;
FilterWithState() = default;
FilterWithState(const typename TFiltBase::Config &c) { Init(c); }
virtual ~FilterWithState() = default;
bool Init(const typename TFiltBase::Config &c) {
return TFiltBase::Init(c, (TArray *)state, TMaxStates);
}
private:
TArray state[TMaxStates];
};Using FilterBoxcar as the filter template parameter for FilterWithState defines FilterBoxcarN as follows,
template<class TArray, int TMaxStates>
using FilterBoxcarN = FilterWithState<FilterBoxcar<TArray>, TMaxStates>If TMaxStates were a template parameter in the original class FilterBoxcar, each variation of this parameter would generate different FilterBoxcar code. The technique of using a thin template wrapper solely to provide state memory avoids regeneration of base class code that has most of the implementation.
Now FilterBoxcarN is a flexible and easy to use component for a filtering function. The following code realizes a single-channel boxcar filter for a SAMPLE_TYPE of double with a configurable length for the running sum up to BOXCAR_LEN samples.
using SAMPLE_TYPE = double;
constexpr int BOXCAR_LEN = 32;
using FILT_BOXCAR = DSP::FilterBoxcarN<SAMPLE_TYPE, BOXCAR_LEN>;
FILT_BOXCAR::Config boxcarCfg;
FILT_BOXCAR boxcar(boxcarCfg);
SAMPLE_TYPE sampleIn, sampleOut;Calling the following line iteratively in a loop runs the filter,
sampleOut = boxcar(sampleIn);
To filter a time sequence where each time sample is a 2D array of signals, change the FilterBoxcarN sample type parameter to a 2D array of some sort as follows,
SAMPLE_TYPE = Eigen::Matrix<double, 4, 4>;
The same one line of code that runs the filter for input/output samples that are of type double, now runs the filter for input/output samples that are an array type, where each array sample consists of the entries in a 2D Eigen matrix. Processing requires an add and a subtract operation per array entry for this multichannel filter, and internally there is circular buffer management of the 3D state that avoids unnecessary data copies.
Templates often provide information or employ conventions about data types and type traits to support the use of one template within another. For example, the following code line,
using Scalar = typename Math::TraitsNumber<TArray>::value_type;
allows class FilterBoxcar to determine the scalar number type being used by TArray.
A template that uses class FilterBoxcar can determine its basic number type via FilterBoxcar<TArray>::Scalar, a convention of the Eigen library [5]. The array type holding the multi-channel signal sample is given by FilterBoxcar<TArray>::value_type, a convention of the Boost C++ libraries [7].
Fig. 2 shows a signal processing pipeline that implements P(H) of Eq. 1. The operator z-D is a D sample delay. Delay operators compensate for an (N-1)/2 delay through each boxcar H of length N. Polynomial coefficients are scaled by powers of N to compensate for the DC gain N of each boxcar filter. For simplicity, gain compensation is illustrated with the coefficients, but gain compensation could be applied elsewhere, such as after the output of H2, or it could also be division instead of multiplication to achieve a normalized gain of 1. For fixed point arithmetic, N is often chosen to be a power of two so that a barrel shift can perform the gain equalizing multiplication or division.
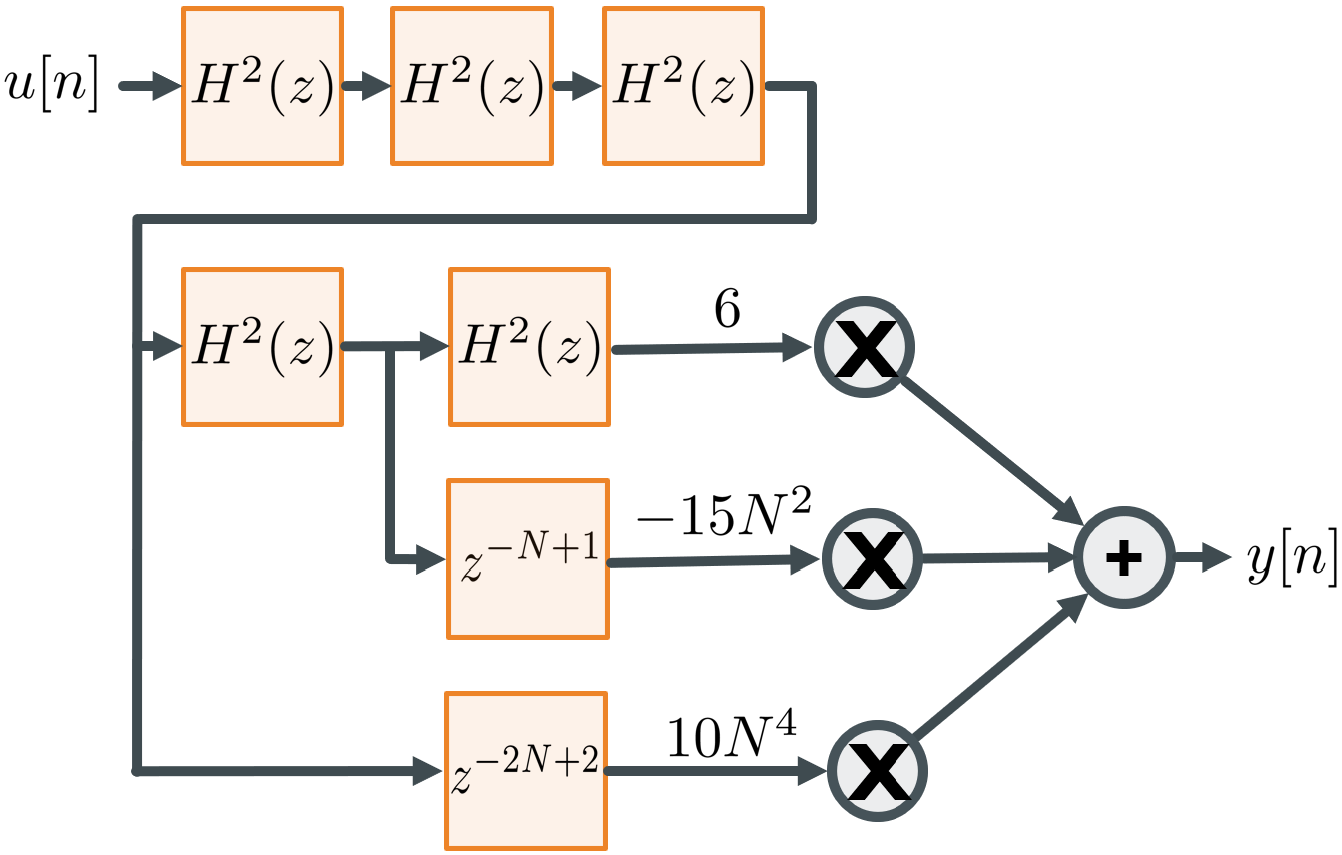
Figure 2: Polynomial filter pipeline for Eq. 1
The FilterSharpenedPoly10 template shown in the listing below implements this pipeline using any filter for its template parameter TFilt that conforms to interface conventions discussed above.
template<class TFilt, int TMaxDelay>
class FilterSharpenPoly10 {
public:
enum {
NUM_FILTS = 10,
};
using T = typename TFilt::Scalar;
using ARRAY = typename TFilt::value_type;
using Config = typename TFilt::Config;
static constexpr T POLY_B0 = static_cast<T>(6.0);
static constexpr T POLY_B1 = static_cast<T>(-15.0);
static constexpr T POLY_B2 = static_cast<T>(10.0);
FilterSharpenPoly10(const Config &c) {
Init(c);
}
virtual ~FilterSharpenPoly10(){ }
bool Init(const Config& c);
// Set/get configuration.
bool Set(const Config& c) { return Init(c); }
// Each component filter is configured the same.
bool Get(Config& c) const { return filter[0].Get(c); }
int operator()(ARRAY &out, ARRAY &in);
// Return DC gain.
T GainDc()const { return gain; }
// Return time delay (centroid of impulse response) in number of sample periods.
T Delay() const { return static_cast<T>(NUM_FILTS*filter[0].Delay()); }
private:
int delay1;
int delay2;
T scale0;
T scale1;
T scale2;
T gain;
TFilt filter[NUM_FILTS];
// States required to compute final output.
ARRAY state1[TMaxDelay*2];
ARRAY state2[TMaxDelay*4];
int idx1=0;
int idx2=0;
// Circular state buffer index increment.
void Inc1(int& i) const { i = ((i + 1) == delay1) ? 0 : i + 1; }
void Inc2(int& i) const { i = ((i + 1) == delay2) ? 0 : i + 1; }
};
template<class TFilt, int TMaxDelay> bool
FilterSharpenPoly10<TFilt,TMaxDelay>::Init(const Config &c)
{
for (int i = 0; i < NUM_FILTS; i++) {
if( filter[i].Init(c) != true)
return false;
}
delay1 = static_cast<int>(2.0*filter[0].Delay());
delay2 = 2 * delay1;
scale0 = filter[0].GainDc() * filter[0].GainDc();
scale0 = static_cast<T>(1.0) / scale0;
scale1 = scale0;
scale2 = scale0 * scale0 * scale0;
scale0 *= POLY_B0;
gain = static_cast<T>(1.0);
idx1 = 0;
idx2 = 0;
return true;
}
template<class TFilt, int TMaxDelay> int
FilterSharpenPoly10<TFilt, TMaxDelay>::operator()(ARRAY &out, ARRAY &in)
{
out = state1[idx1];
out += state2[idx2];
state2[idx2] =
filter[5](filter[4](filter[3](filter[2]((filter[1](filter[0](in)))))))*scale2;
state1[idx1] = filter[7](filter[6](state2[idx2]))*scale1;
out += filter[9](filter[8](state1[idx1]))*scale0;
state1[idx1] *= POLY_B1;
state2[idx2] *= POLY_B2;
Inc1(idx1);
Inc2(idx2);
return 1;
}The following code realizes the FilterSharpenedPoly10 using a NUMBER type double with a configurable BOXCAR_LEN for the maximum running sum of its 10 component FilterBoxcarN objects. The configurable length of the running sum sets the lowpass frequency cutoff of the filter, where a longer sum implies lower cutoff.
using NUMBER = double; // Number type.
constexpr int NUM_CHANS = 12;
constexpr int BOXCAR_LEN = 64;
using ARRAY = Eigen::Matrix<NUMBER, NUM_CHANS, 1>;
using FILTER = DSP::FilterBoxcarN<ARRAY, BOXCAR_LEN>;
using FILTER_SHARP = DSP::FilterSharpenedPoly10<FILTER, BOXCAR_LEN>;
const FILTER::Config cfg(BOXCAR_LEN);
FILTER_SHARP lowpass(cfg);Calling the following line iteratively in a loop runs the filter,
sampleOut = lowpass(sampleIn);
This is a multi-channel filter where each data sample is a 1D ARRAY of length NUM_CHANS.
Figure 3 shows the boxcar filter frequency response for a normalized gain, sampling frequency of 1, and N=8, showing that it is a lowpass filter, albeit perhaps a not so good one by not being very flat in the passband and only having about 16 dB attenuation in the stopband. However, a much higher quality filter results when FilterBoxcarN is used as the TFilt template parameter of FilterSharpenedPoly10. The resulting P(H) has a significantly flatter passband with 60 dB of stopband attenuation. The 3 coefficients of P(H) imply 3 multiplies per sample array element as well as 20 additions/subtractions from 10 boxcar filters concatenated to form the H10 highest order polynomial term.
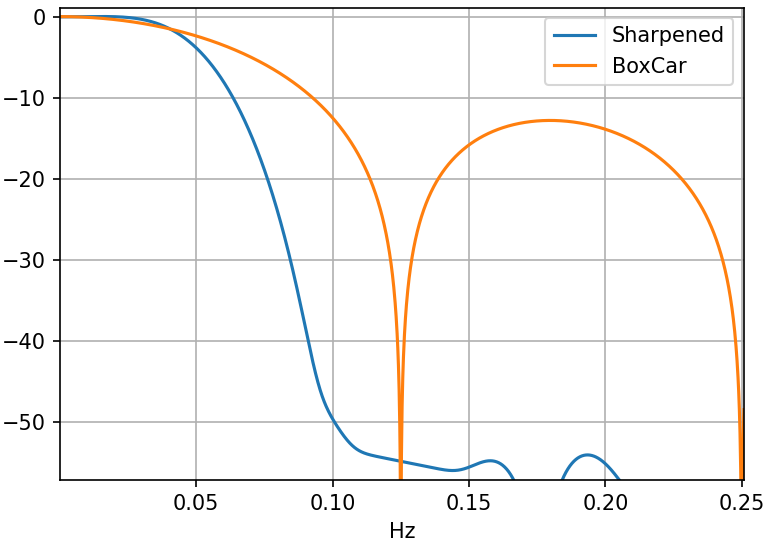
Figure 3: Polynomial filter pipeline for Eq. 1
If one were using fixed-point arithmetic, note that the 3 polynomial coefficients could be implemented without explicit general multiplication. They are easily computed using shifts (multiply by powers of 2) followed by add or subtract. E.g. multiply by 6 using a shift by 2, a shift by 1, and then add the two results. Multiply by 15 using a shift by 4 and subtracting the original number from this result. Note also that these coefficients have relatively few significant digits and hence are relatively insignificant contributors to overflow and truncation.
Figure 4 illustrates the lowpass filter bandwidth for a normalized sampling frequency fs=1, which can be tuned by selecting the running average length N of the Boxcar filter.
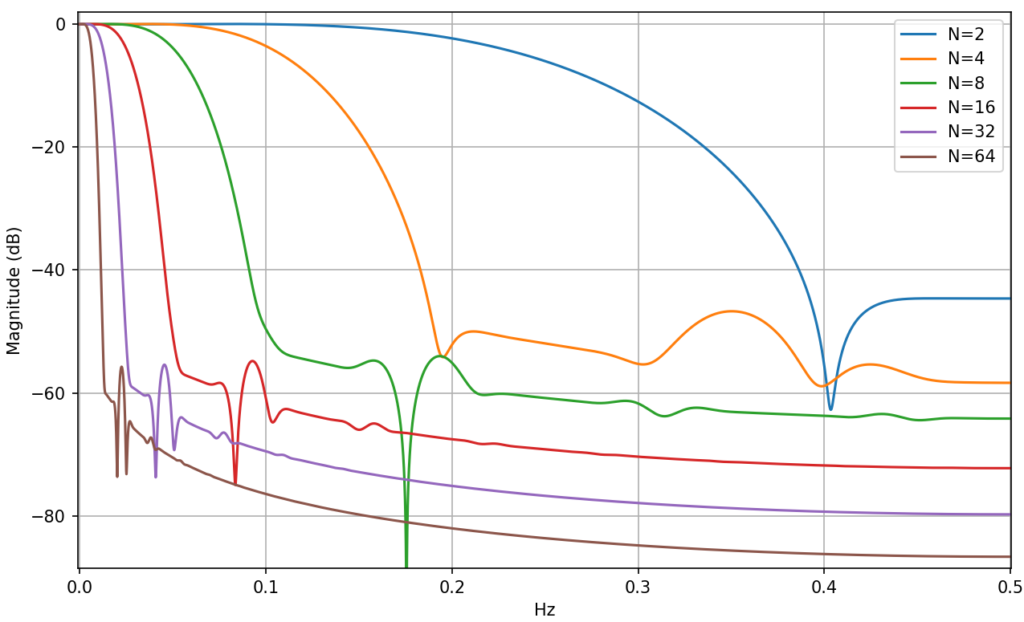
Figure 4: Lowpass filter frequency response magnitude
Runtime Configuration
The high-reliability templates discussed above offer compile-time flexibility in creating variable-sized filters with varying numbers of data channels, all without relying on heap-style allocation. However, what happens if the desired number of channels is only known at runtime say after some user configuration input? Allocating a maximum expected number of channels using template parameters at compile time is an option, but this could lead to unnecessary memory usage as well as extra code complexity if conditionals are added to avoid significant computational overhead for filtering unused channels.
For real-time applications that are less resource constrained where dynamic allocation and heap usage is not a significant concern or where perhaps dynamic allocation is done at startup for configuration only, an alternative general solution is to create a dynamic version of the filters by inheriting from the corresponding flexible template versions and passing them dynamically created buffers or objects, as shown by the FilterBoxcarDynamic and FilterSharpenPoly10Dynamic examples below:
#ifdef ESF_DYNAMIC_MEMORY
#include <memory>
template<class TArrayDynamic>
class FilterBoxcarDynamic : public FilterBoxcar<TArrayDynamic> {
public:
using BASE = FilterBoxcar<TArrayDynamic>;
FilterBoxcarDynamic() = default;
virtual ~FilterBoxcarDynamic() = default;
bool Init(const typename BASE::Config& c, int numChannels, int stateLen) {
// Create memory for the state buffer.
pBuf = std::make_unique<TArrayDynamic[]>(stateLen);
// Initialize the state buffer.
for (int i = 0; i < stateLen; ++i)
pBuf[i].resize(numChannels);
// Initalize the running sum.
BASE::sum.resize(numChannels);
// Initialize the base filter.
return this->BASE::Init(c, pBuf.get(), stateLen);
}
private:
std::unique_ptr<TArrayDynamic[]> pBuf;
};
#endif#ifdef ESF_DYNAMIC_MEMORY
#include <memory>
template<class TFilt, int TMaxDelay>
class FilterSharpenPoly10Dynamic : public FilterSharpenPoly10<TFilt, TMaxDelay> {
public:
using BASE = FilterSharpenPoly10<TFilt, TMaxDelay>;
FilterSharpenPoly10Dynamic() = default;
virtual ~FilterSharpenPoly10Dynamic() = default;
// Disable copy constructor and copy assignment operator
FilterSharpenPoly10Dynamic(const FilterSharpenPoly10Dynamic&) = delete;
FilterSharpenPoly10Dynamic& operator=(const FilterSharpenPoly10Dynamic&) = delete;
bool Init(const BASE::Config& c, int numChannels) {
for (int i = 0; i < BASE::NUM_FILTS; i++) {
if (!this->filter[i].Init(c, numChannels, TMaxDelay))
return false;
}
for (int i = 0; i < TMaxDelay * 2; i++) {
this->state1[i].resize(numChannels);
SetConstant(this->state1[i],static_cast<BASE::T>(0.0));
}
for (int i = 0; i < TMaxDelay * 4; i++) {
this->state2[i].resize(numChannels);
SetConstant(this->state2[i], static_cast<BASE::T>(0.0));
}
return this->BASE::Init();
}
};
#endifThese dynamic filters support runtime configuration of the number and type of data channels as shown in the following code example.
using NUMBER = double; // Number type.
constexpr int NUM_CHANS = 12;
constexpr int BOXCAR_LEN = 64;
using ARRAY = Eigen::Vector<NUMBER, Eigen::Dynamic>;
using FILTER = DSP::FilterBoxcarDynamic<ARRAY>;
using FILTER_SHARP = DSP::FilterSharpenPoly10Dynamic<FILTER, BOXCAR_LEN>;
const FILTER::Config cfg(BOXCAR_LEN / 4);
ARRAY vecIn;
ARRAY vecOut;
// Specify the number of channels to process.
vecIn.resize(NUM_CHANS);
vecOut.resize(NUM_CHANS);
...
// Create and initialize the lowpass filter.
auto pLowpass = std::make_unique<FILTER_SHARP>();
if (!pLowpass->Init(cfg, NUM_CHANS)) {
printf("Error: Failed to initialize the lowpass filter.\n");
return;
}
// Iteratively process.
while( !done ) {
// Fill in vecIn with data.
...
// Run filter
(*pLowpass)(vecOut, vecIn);
...
// Use filtered vecOut output data.
}
Because dynamic filter templates use standard C++ library smart pointers, a conditional compile parameter ESF_DYNAMIC_MEMORY allows us to exclude them for very resource constrained applications. This can help to avoid or minimize dependencies on the standard C++ library that may otherwise increase required ROM or RAM space.
Other Linear Filters
Any basic linear filter can be implemented in a similar manner. The following example demonstrates an auto-regressive moving average (ARMA) filter, also known as an infinite impulse response (IIR) digital filter. Note that an estimate of the filter’s input/output (I/O) signal delay is derived from its coefficients that estimates the centroid of its impulse response. For a Finite Impulse Response (FIR) filter with a symmetric impulse response, this delay is exact and equals half the length of the impulse response. However, in an IIR filter, the nonlinear phase causes different frequencies to pass through the filter with varying time delays, making the concept of a single I/O delay more of an approximation. This approximation may be less meaningful, especially in a high-pass filter where the smaller delay of high frequencies is often more critical.
template<typename TArray>
class FilterArma : public DSP::FilterBase<TArray> {
public:
using value_type = TArray;
using NUM_TYPE = typename DSP::FilterBase<TArray>::NUM_TYPE;
struct Config
{
Config(const NUM_TYPE *b=nullptr, const NUM_TYPE *a=nullptr, size_t n=0)
: b(b), a(a), n(n){}
// Feedforward coefficients: b0, b1, ..., b_(n-1)
const NUM_TYPE *b;
// Feedback coefficients: 1, a1, ..., a_(n-1), a[0] is assumed to be 1.
const NUM_TYPE *a;
// Number of feedforward coefficients = Number of feedback coefficients.
// Use zeros to equalize if needed.
size_t n;
};
explicit FilterArma() = default;
virtual ~FilterArma() = default;
// pS must have length greater than Config::n.
bool Init(const Config& c, TArray* pS) {
NUM_TYPE sb{};
NUM_TYPE skb{};
NUM_TYPE sa{};
NUM_TYPE ska{};
cfg = c;
pState = pS;
for (int i = 0; i < cfg.n; i++) {
sb += cfg.b[i];
skb += cfg.b[i] * i;
sa += cfg.a[i];
ska += cfg.a[i] * i;
SetConstant(pState[i], static_cast<NUM_TYPE>(0.0));
}
// The filter's impulse response centroid or center of mass.
delay = std::abs((sb * ska - sa * skb) / (sb * sa));
// DC I/O amplitude gain of the filter.
gainDC = sb / sa;
return true;
}
// Return one (vector/matrix) sample out for one sample in.
TArray operator()(const TArray &in) {
TArray v;
// This convention adopted from the Eigen matrix library.
SetConstant(v, static_cast<NUM_TYPE>(0.0));
pState[0] = in;
for (int i = cfg.n - 1; i > 0; i--) {
pState[0] -= pState[i] * cfg.a[i];
v += pState[i] * cfg.b[i];
pState[i] = pState[i - 1];
}
return(pState[0] * cfg.b[0] + v);
}
int operator()(TArray &out, const TArray &in){
out = operator()(in);
return 1;
}
// Return filter input/output delay in number of samples.
NUM_TYPE Delay() const { return delay; }
private:
Config cfg;
NUM_TYPE delay; // An estimate of the input output delay.
NUM_TYPE gainDC; // DC gain of the filter.
TArray* pState; // Filter state buffer has size cfg.n.
};An IIR supporting a dynamic number of data I/O channels would be:
#ifdef ESF_DYNAMIC_MEMORY
#include <memory>
template<typename TArrayDynamic>
class FilterArmaDynamic : public DSP::FilterArma<TArrayDynamic> {
public:
using BASE = FilterArma<TArrayDynamic>;
FilterArmaDynamic() = default;
virtual ~FilterArmaDynamic() = default;
// numChannels is the number of data channels filtered in
// in parallel
bool Init(const typename BASE::Config& c, int numChannels) {
// Create memory for the state buffer.
pBuf = std::make_unique<TArrayDynamic[]>(c.n);
// Initialize the state buffer.
for (int i = 0; i < c.n; ++i)
pBuf[i].resize(numChannels);
// Initialize the base filter.
return this->BASE::Init(c, pBuf.get());
}
private:
std::unique_ptr<TArrayDynamic[]> pBuf;
};
#endifConclusion
This first installment offers a glimpse of more comprehensive content to come, where we’ll continue to demonstrate how C++ can achieve levels of abstraction and high-level functionality comparable to Python or MATLAB, while preserving efficiency close to hand-crafted C. In fact, the abstractions we discuss here that support efficient real-time, iterative data streaming and data streaming operators, are higher-level than the matrix/vector abstractions in Python or MATLAB, for example. Moreover, these concepts are typically not the focus of libraries in those languages.
Many programmers of resource constrained embedded systems are concerned about C++ templates causing “code bloat”, a topic we’ve briefly touched upon when we demonstrated the “thin wrapper template technique” for managing filter state where a template parameter specifies the amount of state. In the wrapper approach, a template with many parameter variations is wrapped around a base class without these parameters, but which handles most of the work. This limits the compile time generation of code for each variation of the parameters to a small amount of wrapper code only. Additionally, we discussed the option of avoiding dependencies on certain resource-intensive standard C++ libraries. Although we haven’t fully addressed this concern yet, we will revisit it in future installments. We will argue that with proper template techniques, not only can code bloat be avoided, but effective template usage is more likely to result in code shrinkage, as the compiler automatically eliminates unused template class methods.
See Part II for continued development of these methods.
Bibliography
- [1] Valery Ignatov. “C++ template metaprogramming for AVR microcontrollers”. Embedded.com Oct. 19, 2016.
- [2] Github ESF link (coming soon).
- [3] Alexander Holland, [Online]. Available: Signal Conditioning with Almost No Multiplications via Filter Sharpening | IEEE Conference Publication | IEEE Xplore
- [4] M. Danadio [Online]. Available: Lost knowledge refound: sharpened FIR filters | IEEE Journals & Magazine | IEEE Xplore
- [5] https://eigen.tuxfamily.org/
- [6] Eigen – Arduino Reference
