Introduction
Part I introduced a C++ template strategy for efficiently and effectively implementing general real-time signal processing computational pipelines or networks. These pipelines can form a hierarchy of different operator types connected in a network, operating on signals of various types. As an initial example, we focused on computational pipelines with multi-channel linear digital filters. We demonstrated how to construct these filters with relative ease, without the need for complex software machinery or heap allocation.
In this installment, we turn our attention to the two main components of a digital signal processing computational pipeline: signals and computational operators. We discuss their properties and our implementation models for them in more detail, demonstrating both concrete and abstract tactics and strategies for their efficient realization.
Signals in the context of digital processing by a computer, are 1D, 2D, 3D, or nD data arrays or other application-specific data structures or types, sampled or updated at discrete time points. These signals typically begin as sensor measurements of physical phenomena, such as voltages, sounds, or images, and may then progress through multiple computational stages to yield higher-level or derived properties from the initial measurements, such as waveform features or classifications. For example, in an electrocardiogram (ECG), signals might include the location and classification of each QRS complex as a normal beat or as indicative of a specific type of arrhythmia. Data may be acquired at different sample rates or processed so that it is spaced at non-uniform time intervals. In such cases, a time dimension or data structure field explicitly contains the non-uniformly spaced time values of the array data samples.
In most cases, a 1D mathematical vector:
\mathbf{u}[k] = \left[u_0[k], u_1[k], \ldots, u_{M-1}[k] \right]^T
is sufficient to represent M data samples (e.g., from M sensors) taken at the same point in time, where integer k identifies the time and
k = 0, 1, \ldots,
distinguishes each vector sample collected sequentially in time. Given the data sampling frequency f_s in units of hertz (Hz), the true time of the data sample relative to the first sample at k=0 would be
t_k = k / f_s
The highest value of k represents the total number of vector data samples collected. The time varying vector \textbf{u}[k] is thus defined as a discrete time mathematical signal. Specifically in our context, it is an input signal for a computational operator \mathbf{G} that processes it to produce output signal \mathbf{y}[k] :
\mathbf{y}[k] = \mathbf{G}(\mathbf{u}[k])
More complex signals may consist of sample vectors that are multidimensional or non-uniformly spaced in time, requiring additional indices to represent or a more intricate organization, such as explicit time values for varying time intervals between samples. Our templates are designed to handle these complexities effectively, and we will explore these aspects in detail when necessary. For simplicity, however, we can often conceptualize higher-dimensional data types as flattened into vectors because the fundamental processing implementation and strategy remains largely unchanged. When dealing with higher order tensors, for example, the main implementation difference is usage of a tensor sample type instead of a vector type in the computational operator template.
Time Windows and State
We can observe real-time signal samples from the present and past but not from the future. The history of these observations is referred to as a time “window” which, in theory, could extend infinitely into the past. However, in practice, it starts when data acquisition begins in a physical instrument. Real-time computation typically requires processing data within a fixed-size time window of N data samples. At any given current time k, the data samples available for computation are
\mathbf{u}[k-N+1], \mathbf{u}[k-N+2], \ldots, \mathbf{u}[k-1], \mathbf{u}[k] .
The current data window accessible to an operator can be represented as an N \times M 2D array or matrix, where each row is a vector data sample.
Saving and processing an ever-growing data buffer, instead of using a fixed sized window for example, could not only risk memory issues but also increase computational latency and overhead as the system operates. This could potentially lead to unexpected real-time failures that are generally undesirable.
To account for past data outside the current time window, a common strategy is to use a state variable vector,
\mathbf{x}[k] = \left[x_0[k], x_1[k], \ldots, x_{P-1}[k] \right]^T
to represent and summarize the net effect of the past via a state update operator:
\mathbf{x}[k+1] = \mathbf{F}(\mathbf{x}[k], \mathbf{u}[k])
The operator \mathbf{F} computes the next state \mathbf{x}[k+1] from the current state \mathbf{x}[k] and the input \mathbf{u}[k]. When summarizing past data, \mathbf{F} often assigns greater weight to recent data compared to data from the more distant past, as is common in linear filters. The state also serves as an additional input for the output operator, which now computes the output signal \mathbf{y}[k] from both \mathbf{u}[k] and \mathbf{x}[k]:
\mathbf{y}[k] = \mathbf{G}(\mathbf{x}[k], \mathbf{u}[k])
Ring Buffers
To avoid unnecessary data copying, a common software tool for managing the N \times M time window matrix is the “ring buffer”. In its simplest form, the ring buffer maintains a row index, n \in \{ 0, 1, \ldots, N-1 \} , which points to the oldest sample vector in the matrix. The following code lines from the boxcar filter shown in Part I illustrate a simple ring buffer. pState is initialized with maxN rows and M columns, while idx (n) identifies the oldest sample vector in the ring.
TArray* pState = nullptr;
size_t maxN=0;
size_t idx=0;
void Inc(size_t& i) const { i = ((i + 1) == cfg.N) ? 0 : i + 1; }The operator uses the current n to (1) initiate an iterative computation cycle with the oldest sample, (2) replace the oldest sample with the newly acquired input sample vector, and (3) increment n modulo N so that it continues to point to the oldest sample when the operator begins again at step (1) in the next iteration. Many of the basic filter (operator) examples in Part I followed this pattern.
The use of a ring buffer eliminates the need to shift matrix rows to maintain the current time window in the same row locations, thereby avoiding a potentially significant overhead that can occur from inner computation loops to throughout the computational pipeline. However, using a ring buffer requires that processing be designed to accommodate the circular buffer index n, which accesses data starting at a different row on each iteration and wraps back to the first matrix row after reaching the last row.
Signal Class
In our implementation model, processing any time sequence of any data type using a ring buffer is so central that we support it as a general implementation design pattern via the Signal class, a portion of which is shown below.
template <class TStruct>
class Signal
{
public:
/// Common convention to export the basic number type.
using value_type = TStruct;
using NUM_TYPE = typename Math::TraitsNumber<TStruct>::value_type;
using T = NUM_TYPE;
Signal(TStruct* p, int len) : pBuf(p), bufSize(len) { Init(); }
virtual ~Signal(void) = default;
void Init()
{
IndexSet(0); // First empty position.
WrapsSet(0); // Number of circular buffer wraps.
}
// Return a pointer to the raw data buffer.
TStruct* RawData() { return pBuf; }
/// Return sample vals from the oldest (i=0) to the newest (i=bufSize-1).
TStruct& operator[](const int& i) { return pBuf[Index(i)]; }
/// Return sample vals from beginning (i=0) to end (i=bufSize-1) of the buf.
TStruct& operator()(const int& i) { return pBuf[i]; }
/// Return number of samples that could be stored in the signal without overflow.
unsigned BufSize() const { return bufSize; }
/// Return the number of samples in the current signal time window.
/// This will be less than bufSize until the signal is full, and then
/// will be equal to bufSize.
unsigned NumSamples() const { return IsFull() ? BufSize() : index; }
/// Return a count of the total number of samples that have been stored
/// in the signal, including those that have been overwritten.
unsigned TotalSampleCount() const { return IndexWithWraps(); }
/// If false, processing is still in an initialization transient period.
/// If true, processing is in steady-state.
bool IsFull() const { return IndexWithWraps() >= BufSize(); }
// Return the current sample value.
TStruct Value() const { return operator()(index); }
/// Return the current sample index.
int Index() const { return index; }
/// Return the sample index corresponding to current time (offset = 0),
/// later samples times (offset > 0) or earlier sample times (offset < 0).
/// Count and return circular buffer wrappings in *pWrap.
int Index(int offset, int32_t* pWraps = NULL) const { return IndexModuloSize(index + offset, pWraps); }
/// Return the sample index accounting for circular buffer wrappings.
unsigned IndexWithWraps(int offset = 0) const
{
int32_t offsetWraps;
int idx = Index(offset, &offsetWraps);
// Add the circular buffer wrappings to the index.
idx += (Wraps() + offsetWraps) * BufSize();
return (unsigned)idx;
}
/// Increment 'index' modulo BufSize(). Use to support circular
/// operations ("tapped delay line") of sample vectors.
int IndexNext()
{
if ((index + 1) == static_cast<int>(BufSize()))
{
index = 0;
wraps += 1;
}
else
index += 1;
return index;
}
/// Decrement 'index' modulo BufSize(). Use to support circular
/// operations ("tapped delay line") of sample vectors.
int IndexPrev()
{
if (index == 0)
{
index = BufSize() - 1;
wraps -= 1;
}
else
index -= 1;
return index;
}
/// Increment sample 'index' modulo BufSize(). Use to support circular
/// operations ("tapped delay line") of sample vectors.
int IndexInc(int t)
{
index += t;
while (index >= static_cast<int>(BufSize()))
{
index -= BufSize();
wraps += 1;
}
return index;
}
/// Decrement sample 'index' modulo BufSize(). Use to support circular
/// operations ("tapped delay line") of sample vectors.
int IndexDec(int t)
{
index -= t;
while (index < 0)
{
index += BufSize();
wraps -= 1;
}
return index;
}
/// Set the sample index to 'val'.
int IndexSet(int val)
{
index = val;
return index;
}
/// Set the sample index to 'val' and count buffer wrappings.
int IndexSetWithWraps(int32_t val)
{
index = IndexModuloSize(val, &wraps);
return index;
}
/// Return the number of times the internal circular buffer wrapped.
long Wraps() const { return wraps; }
/// Set the number of times the internal circular buffer has wrapped.
void WrapsSet(long val = 0) { wraps = val; }
/// Return the number of samples until the end of the circular data buf
/// is reached, or return 'len' if the end is not reached.
int SamplesToEnd(int len) const { return std::min(static_cast<int>(BufSize()) - index, len); }
/// Determine if adding 'len' elements would reach the end of the internal
/// circular buffer.
int AtEnd(int len) const { return ((index + len) >= BufSize() ? true : false); }
/// Copy 'len' data values from the 'in' signal to this signal.
Signal& Append(const Signal& in, int len);
/// Circularly append 'pDta'. "Wrap" to append up to the
/// maximum number of samples in the signal.
Signal& Append(const TStruct* pDta, int len);
/// Copy 'len' data values of the 'in' signal to
/// to this signal in reverse time order.
/// Note that 'in' should be a signal different from this one.
/// Use Reverse() to reverse the order of the samples in the same signal.
Signal& AppendReverse(const Signal& in, int len);
/// Circularly append 'pDta' in reverse time order.
/// "Wrap" to append up to the maximum number of samples in the signal.
Signal& AppendReverse(TStruct* pDta, int len);
/// Starting from the present position specified by index, reverse the
/// order of the next 'len' values. 'len' should be less
/// than or equal to BufSize().
Signal& Reverse(int len);
/// Fill 'pDta' with data from current position. "Wrap" if necessary.
Signal& Get(TStruct* pDta, int len);
private:
int index; // Oldest sample index or the head.
int32_t wraps; // Number of ring buf "wrappings" since the last reset.
TStruct* pBuf;
int bufSize;
// !!! Make sure that b > 1.
static int FloorAdivB(int a, int b)
{
if (a < 0)
return (a + 1) / b - 1;
else if (a >= b)
return a / b;
else
return 0;
}
/// Find the difference between the two indices, where idxA is
/// assumed to correspond to a later sample than idxB.
int IndexDiff(int idxA, int idxB) const { return IndexModuloSize(idxA - idxB); }
/// Return the index that is congruent to the given index
/// modulo the size or number of samples in the buffer.
int IndexModuloSize(int32_t idx, int32_t* pWraps = NULL) const
{
int tmp = BufSize();
int32_t cnt;
// Need cnt = floor(idx/tmp) for negative indices,
// i.e. cnt = floor(-3/5) = -1.
cnt = FloorAdivB(idx, tmp);
idx -= cnt * tmp;
if (pWraps != NULL) *pWraps = cnt;
return idx;
}
};This class provides support for circular data processing to reduce the need for data copies. The Signal is viewed as having a fixed number of samples representing a finite window of time. A new sample generally replaces the oldest sample, identified by the index field. Initially, the samples may contain random data, leading to a transient period until the buffer is full. After the buffer is filled, replacing old samples with new ones represents steady-state operation. Class methods include support for (a) retrieving the oldest or newest data samples, (b) moving samples into and out of the Signal, (c) determining how far the current sample is from the end of the Signal (is the number of samples that are contiguous before wrapping), and (d) providing a count of the total samples processed as well as finding a sample index that accounts for Signal buffer wraps or multiple overflows.
Note that the linear filter operator examples presented previously did not use the Signal class internally to implement their signal ring buffers. Although this could have been done, we generally choose to employ abstract machinery only when simple and direct methods are insufficient. The objective of any abstract software machinery is to make complex implementations easier, not to make simple implementations harder. For this reason, abstract code is not used for simple tasks where it may technically apply but tends to obscure rather than assist.
General Computational Operator Model
Figure 1 illustrates this real-time computational operator model. In addition to maintaining a finite N \times M signal time window for the input \textbf{u}[k], it also keeps a finite L \times P signal time window for the state vector \textbf{x}[k] by storing the last L state vectors.
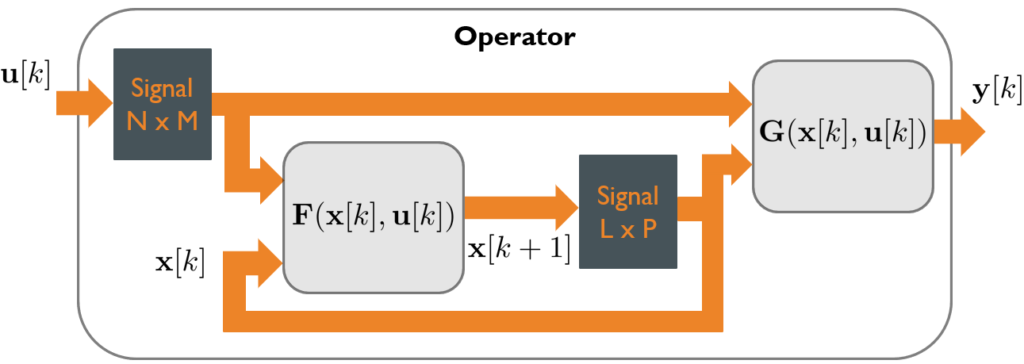
Figure 1: General model for a real-time computational operator
Although the general multi-input, multi-output functions \mathbf{F}(\mathbf{x}[k],\mathbf{u}[k]) and \mathbf{G}(\mathbf{x}[k],\mathbf{u}[k]) are depicted as functions of the entire input and state signals, they should be understood as only having access to the signal and state values stored in the respective signal ring buffers connected to their inputs. This general computational model is applicable to many signal-processing functions, including linear filters, Kalman filters, nonlinear regression, support vector machines, convolutional neural networks, etc.
There is a transient operation period during which the signal ring buffers fill up, after which the operation enters a steady state. If the designs of \mathbf{F} and \mathbf{G} employ algorithms with deterministic computational characteristics and latencies, and if implementations exclude sources of highly variable latencies—such as heap based dynamic memory allocation—then the computational performance statistics will be more stable in steady state operation, with reduced variability around the mean.
