Suppose one desires to sense and measure an analog physical signal where direct access is difficult or costly due to extreme heat, safety, or other reason. A typical objective is to obtain digital data samples s_o[k] = s_0(t=k/f_s), \; k = 0, 1, 2, \ldots with as little noise or artifact as possible. Typically, the emphasis is on sensor and analog-to-digital conversion (ADC) quality – sample rate ( f_s ), resolution, accuracy, etc.
Traditionally, one might try to build a mathematical model to relate s_o[k] to a different signal s_i[k] that he could directly access and sense,
s_o(t) = F(s_i(t), \mathbf{c}, t)
where F(s_i(t), \mathbf{c}, t) may be a function of current and past values of s_i(t) , known and unknown parameters \mathbf{c}, and time t. Sometimes this works, but generally only in limited idealized circumstances. Often modeling fails in practice due to system complexity, nonlinearity, time variance, or due to difficulties in solving mathematical “inverse problems”.
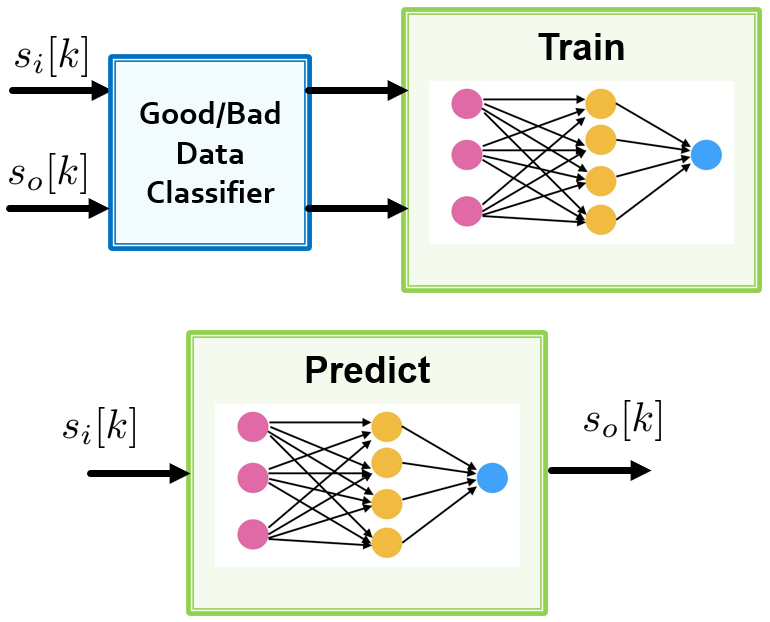
Instead, if one could collect a sufficient and diverse enough quantity of synchronized s_i[k] and s_o[k] data samples, he might solve the modeling problem more effectively by training a machine learning (ML) algorithm as shown in Fig. 1. In principle a deep learning (DL) approach does not require a physical model, but having one may help inspire a particular neural net architecture, and also supports other potential model based learning algorithm options beyond deep learning. Because curating data is often as much or more work than the learning algorithm itself, for constructing training data, it is often useful to build a relatively simple Good/Bad Data Classifier, which could also optionally augment prediction.
Although one would likely be remiss in not evaluating machine learning for improving almost any system, most prominent examples require terabytes or more of data to train neural nets with thousands of parameters that require relatively large and power hungry computers. Tools such as TensorFlow Lite for Microcontrollers help make it possible to apply such methods to the world of small, low-power microcontrollers with kilobytes of memory and relatively weak available computing power. These systems also often support continuous data flow sometimes situated within feedback loops where long computational delays are often not tolerable. The TensorFlow Microcontroller tool trims down neural net size and brings back fixed-point arithmetic to avoid power draw from floating point units. Despite this, achieving a working system in practice remains a challenge.
